首先可以了解一下Monte Carlo 方法，这里是链接https://en.wikipedia.org/wiki/Monte_Carlo_method。

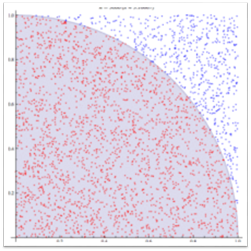
根据圆的面积公式S=πR^2，当R=1时，S=π。
我们在一个边长为1的正方形中划定一个半径为1的1/4圆区域。我们向这个正方形区域内随机投点，根据几何概型（高中数学知识，我在此不再赘述），点落到1/4圆区域内的概率为P=π/4. 这个概率的四倍便可以视为π的近似值。
根据这个思路，我们要想用程序模拟出π的近似值，就可以转换为模拟这样一个几何概型求它的概率的问题。以下是用c语言实现这个过程的代码：

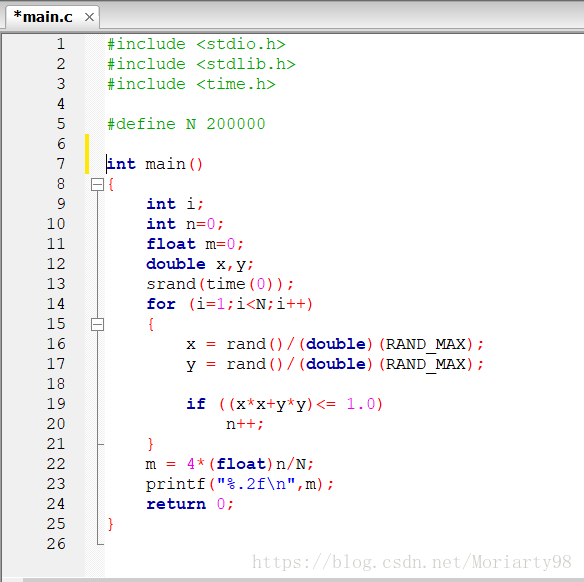
/这个精度有点看概率，一开始我宏定义N为2000,得到了3.16,
改成10000得到了3.19,
改成20000得到了3.17,
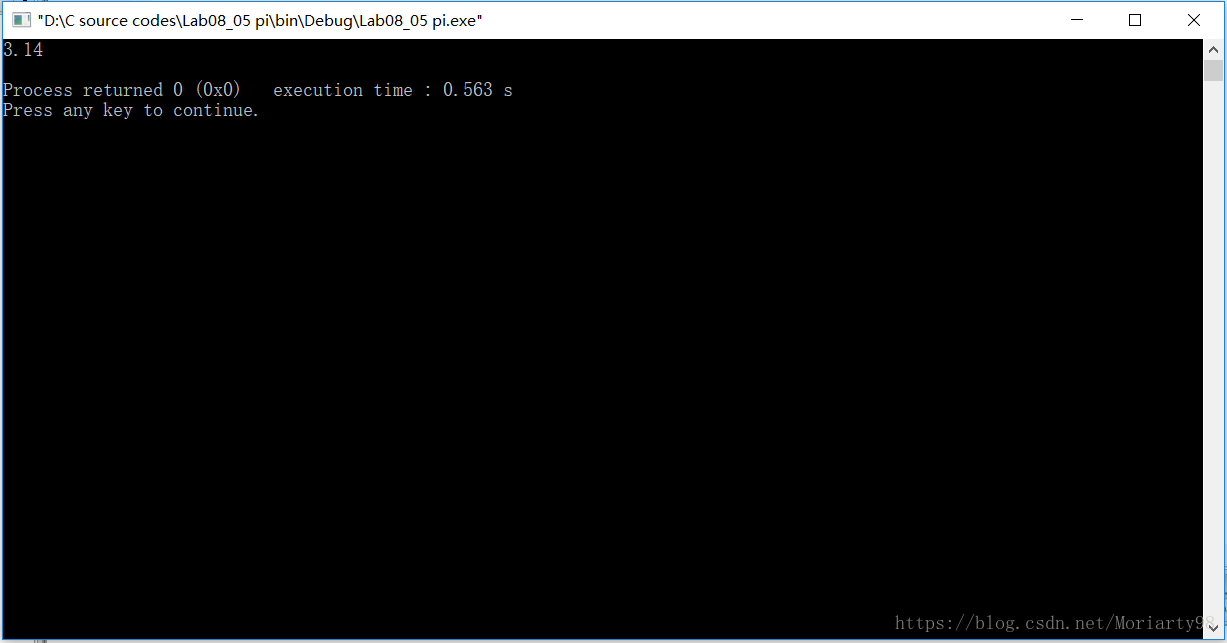
改成200000,得到了3.14,
之后又用200000测试了4次，得到了三次3.14，一次3.13/

最后再简单介绍一下程序中用到的几个函数。如果是像我一样的c语言刚入门学习的小白可能会不太熟悉，详细的用法可以自行翻书查阅。

rand()函数可以产生伪随机数，之所以说是伪随机数是因为rand()函数的内部实现是通过线性同余法实现的，由于其周期较长所以，所以在一定范围内可以看作是随机的。rand()返回的是0-RAND_MAX之间的随机数。调用rand()函数时需要设置随机数种子，如果不设置的话，它自动设置为1，随机数种子相同，产生的随机数也是相同的，这样的达不到我们要用产生随机数模拟投点来求π的近似值的目的了。设置随机数种子需要srand()函数,它是随机数产生器的初始化函数，再利用time函数来返回系统时间作为随机数种子，就可以达到每次随机数种子都不同的目的了。因为每次运行程序的时间肯定是不同的。可以像我上面的程序中那样写为srand(time(0)); ,另一种的常见的用法是直接在time函数中放一个空指针：srand((unsigned)time(NULL))。
rand()和srand()所需的头文件是stdlib.h,time()函数所需的头文件是time.h。
以上全部是我一些粗浅的理解，难免有错误之处，欢迎指正。随着自己学习的深入回过头再看的时候应该会有更好的理解吧。